
Internal Rate of Return
As the word "return" in its name implies, an IRR view of the cash flow stream is essentially an investment view: money will be paid out and compared to money earnt.
Instead of a simple ratio between inflows and outflows (as with ROI), the IRR compares returns to costs by asking:
"What is the discount rate that would give the cash flow stream a net present value of 0 (zero)?"
Instead of a simple ratio between inflows and outflows (as with ROI), the IRR compares returns to costs by asking:
"What is the discount rate that would give the cash flow stream a net present value of 0 (zero)?"
This definition, however, is often less than fully satisfying to most people, especially when hearing it for the first time.
Many people ask: "What does that tell me? How does IRR compare to other metrics such as NPV or to ROI?
Clearly, understanding IRR requires an understanding of the concepts present value (PV), net present value (NPV), and the role of the discount rate (interest rate percentage) in determining NPV.
IRR asks a different question to NPV of two cash flow streams. Instead of proposing a discount rate and finding the NPV of each stream (as we do with NPV), IRR starts with the net cash flow streams and finds the interest rate (the discount rate) that produces an NPV of zero for each cashflow.
The easiest way to see how this solution is found is with a graphical summary. The curves are based on two cashflows Case A and Case B.
Many people ask: "What does that tell me? How does IRR compare to other metrics such as NPV or to ROI?
Clearly, understanding IRR requires an understanding of the concepts present value (PV), net present value (NPV), and the role of the discount rate (interest rate percentage) in determining NPV.
IRR asks a different question to NPV of two cash flow streams. Instead of proposing a discount rate and finding the NPV of each stream (as we do with NPV), IRR starts with the net cash flow streams and finds the interest rate (the discount rate) that produces an NPV of zero for each cashflow.
The easiest way to see how this solution is found is with a graphical summary. The curves are based on two cashflows Case A and Case B.
Here, however, we have used nine different interest rates, 0.0 to 0.80.
As you would expect, as the interest rate used for calculating NPV as the cash flow stream increases, the resulting NPV decreases.
As you would expect, as the interest rate used for calculating NPV as the cash flow stream increases, the resulting NPV decreases.
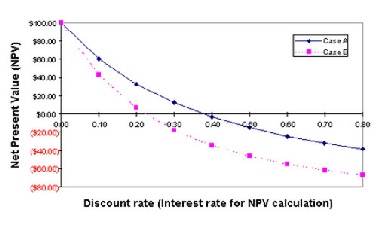
For Case A, an interest rate of 0.38 produces NPV = 0, whereas
Case B NPV arrives at 0 with an interest rate of 0.22.
Case A therefore has an IRR of 38%, and Case B an IRR of 22%.
Which is the better Investment? Other things being equal, and using IRR as the decision criterion, the one with the higher IRR is the better choice.
Another way to think of IRR is this: IRR tells you just how high inflation rates have to go in order to eliminate the present value of this investment.
For the Case A cash flow, the prevailing inflation rate would have to rise to 38% to make this investment worthless.
Whereas Case B investment would become worthless if interest rates rose to 22%.
Instead of finding a graphical solution for IRR, most people today use spreadsheet s such as Microsoft Excel or or OpenOffice or a pre-programmed calculator.
In either case, the software uses an arbitrarily chosen discount rate to find NPV for a given cash flow stream, and then keeps changing the rate (iteration) until it finds a rate that produces a 0 NPV. This occurs very quickly, so that the IRR result seems to appear as soon as the data are entered.
Many Finance Directors use IRR as they can are used to comparing competing investments and calculating the IRR provides an element of risk management, ie how high does inflation need to go to wipe out the benefit of this investment.
Finally IRR can be combined with a Hurdle Rate to ensure that different classes of investment achieve minimum returns or they fail at the Approval Gateway.
Case B NPV arrives at 0 with an interest rate of 0.22.
Case A therefore has an IRR of 38%, and Case B an IRR of 22%.
Which is the better Investment? Other things being equal, and using IRR as the decision criterion, the one with the higher IRR is the better choice.
Another way to think of IRR is this: IRR tells you just how high inflation rates have to go in order to eliminate the present value of this investment.
For the Case A cash flow, the prevailing inflation rate would have to rise to 38% to make this investment worthless.
Whereas Case B investment would become worthless if interest rates rose to 22%.
Instead of finding a graphical solution for IRR, most people today use spreadsheet s such as Microsoft Excel or or OpenOffice or a pre-
In either case, the software uses an arbitrarily chosen discount rate to find NPV for a given cash flow stream, and then keeps changing the rate (iteration) until it finds a rate that produces a 0 NPV. This occurs very quickly, so that the IRR result seems to appear as soon as the data are entered.
Many Finance Directors use IRR as they can are used to comparing competing investments and calculating the IRR provides an element of risk management, ie how high does inflation need to go to wipe out the benefit of this investment.
Finally IRR can be combined with a Hurdle Rate to ensure that different classes of investment achieve minimum returns or they fail at the Approval Gateway.